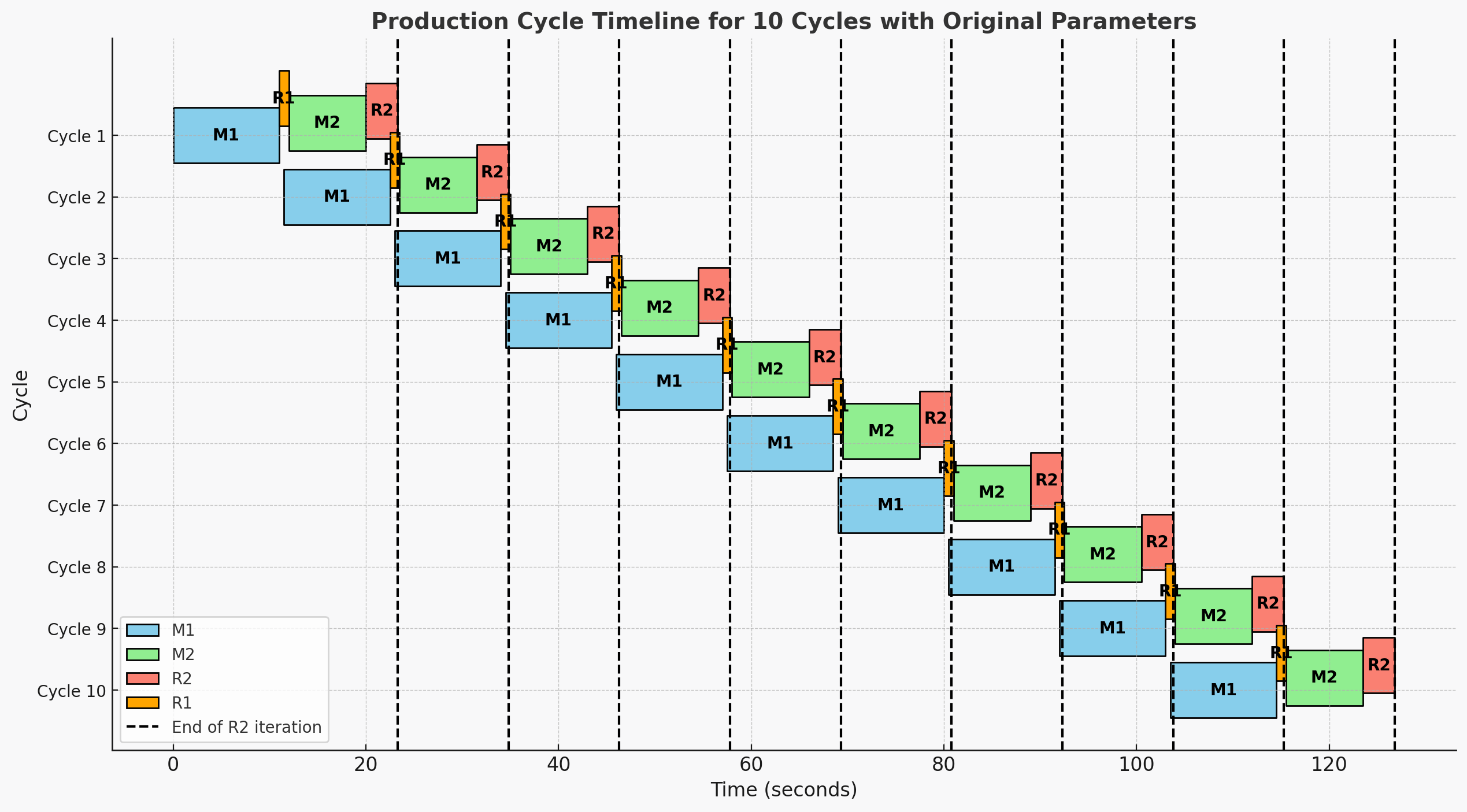
\[ \text{First (n=1):} \begin{cases} T_{\text{start}}^1(M_1) = 0 \\ T_{\text{end}}^1(M_1) = T_{\text{start}}^1(M_1) + T_{M1}\\ T_{\text{start}}^1(R_1) = T_{\text{end}}^1(M_1) \\ T_{\text{end}}^1(R_1) = T_{\text{start}}^1(R_1) + T_{R1} \\ T_{\text{start}}^1(M_2) = T_{\text{end}}^1(R_1)\\ T_{\text{end}}^1(M_2) = T_{\text{start}}^1(M_2) + T_{M2} \\ T_{\text{start}}^1(R_2) = T_{\text{end}}^1(M_2) \\ T_{\text{end}}^1(R_2) = T_{\text{start}}^1(R_2) + T_{R2} \\ \end{cases} \]
\[ \text{Subsequent (n} \geq \text{2):} \begin{cases} T_{\text{start}}^n(M_1) = T_{\text{end}}^{n-1}(R_1) - T_{M1\_overlap} \\ T_{\text{end}}^n(M_1) = T_{\text{start}}^n(M_1) + T_{M1} \\ T_{\text{start}}^n(R_1) = T_{\text{end}}^n(M_1) \\ T_{\text{end}}^n(R_1) = T_{\text{start}}^n(R_1) + T_{R1} \\ T_{\text{start}}^n(M_2) = T_{\text{end}}^n(R_1) \\ T_{\text{end}}^n(M_2) = T_{\text{start}}^n(M_2) + T_{M2} \\ T_{\text{start}}^n(R_2) = T_{\text{end}}^n(M_2) \\ T_{\text{end}}^n(R_2) = T_{\text{start}}^n(R_2) + T_{R2} \end{cases} \]